Differential Privacy is a mathematical framework that prevents an analyst from leaking information when querying a data store. It works by carefully adding noise to the data while preserving the database's global statistical properties. We can get aggregated information without sacrificing individual privacy. As we explore the uncharted territories of privacy in society, who decides what is an acceptable privacy level for citizens? How is it defined? When it comes to privacy, what are the limits? To err on the side of caution, we discussed this topic with the shrewdness of an elder statesman, the diligence of a hacker, and the rigor of a 'street fighting mathematician'.
### **Real-Life Impact of this Research**
+ Talk given at Vancouver meetup titled [Differential Privacy: Foundations and Applications](https://kenluck2001.github.io/static/publications/Privacy-at-your-Fingertips.pdf), 2023.
+ K Odoh, UltraFilter: A Privacy-Preserving Bloom Filter. Proceedings of the International World Wide Web Conference [PDF](https://kenluck2001.github.io/static/publications/kenneth-odoh-ultrafilter-bloomfilter.pdf), 2025.
+ K Odoh, Group-wise K-anonymity meets (ε, δ) Differentially Privacy Scheme. Proceedings of the International World Wide Web Conference [WWW](https://www2024.thewebconf.org/accepted/short-papers/), [PDF](https://kenluck2001.github.io/static/publications/kenneth-odoh-knn-dp.pdf), 2024.
+ K Odoh, Connect the dots: Dataset Condensation, Differential Privacy, & Adversarial Uncertainty, [PDF](https://arxiv.org/pdf/2402.10423.pdf), 2024.
##### Notes:
- Every source code is the author's original work. The accompanying software is done in good faith and makes no claim about the correctness of the solution to the extent possible under the [MIT license](https://opensource.org/license/mit/).
- Repo: https://github.com/kenluck2001/diffprivacy
When there is multicollinearity, using basic anonymization techniques like removing the field may be shortsighted and useless, as the existing field may contain the same information. Even if we get some level of privacy by removing the identifiable field, we still have a problem where we cannot objectively quantify the level of privacy guaranteed. Unfortunately, in this context, enhancing privacy can be challenging as it is difficult to explain privacy losses. There are several privacy-aware methods such as [zero-knowledge proofs](https://en.wikipedia.org/wiki/Zero-knowledge_proof), [homomorphic encryption](https://en.wikipedia.org/wiki/Homomorphic_encryption), and [secure multi-party computation](https://en.wikipedia.org/wiki/Secure_multi-party_computation) which are outside the scope of this work. We present a few case studies to show the applications of differential privacy in frequency estimation and negative databases.
Differential privacy comes to our rescue. It provides a framework for adding structured noise to the data while preserving its statistical properties. The use of differential privacy provides a principled framework for determining how much is required to achieve a target privacy level. There are alternative notions of privacy which include:
+ Putterfish privacy [[7]](): This framework allows non-privacy experts to integrate their domain expertise into privacy definitions, tailored to their specific needs. It has Bayesian statistics foundations. It quantifies the attacker's belief before and after seeing the data. This is analogous to the attacker advantage discussed in the section on the mathematical foundation for the "vanilla" differential privacy mechanism.`
+ Differential identifiability [[8]](): This mechanism aims to prevent the user from specifying $\xi$ which can be error-prone as there is a lack of guidance where inappropriate values may impact privacy guarantees.-* This work can be augmented with ideas from the paper [[6]]() on figuring reasonable privacy bounds on ($\xi, \delta$) which can prevent privacy violations in real-world applications.
Privacy losses can be subtle and challenging to detect. Therefore, differential privacy should be combined with engineering safeguards to enhance data privacy. For example, an individual avoids oversharing by withholding his employer's name on social media (LinkedIn). The individual may inadvertently reveal his employer if a large group of colleagues becomes friends on social media. Another individual (attacker) can use this hint to deduce her employer. However, if your friend list is randomized or friendships are not announced, this information can be preserved. Thus, we can achieve privacy in relation to our employers. The correlation may not give precise information, but it reduces guessing space, resulting in privacy leaks. For example, an individual can be identified using a combination of zip code, gender, and birthday. A single data point alone may not leak anything, but an attacker can build a profile and connect information. This is especially true in this era of security incidents where a future breach may make previously anonymized data re-identifiable.
Privacy protections are prevalent in the jurisprudence of several countries. For example, the [4th Amendment](https://constitution.congress.gov/constitution/amendment-4/) in the United States Constitution, protects citizens from unnecessary searches by the government. [Section 37](https://www.constituteproject.org/constitution/Nigeria_1999.pdf) of the Nigerian constitution guarantees citizens the right to privacy. [Section 8](https://www.canada.ca/content/dam/pch/documents/services/download-order-charter-bill/canadian-charter-rights-freedoms-eng.pdf) of the Canadian Charter of Rights and Freedoms protects Canadians from arbitrary searches by the authorities. Software engineers stand to financially benefit from increased privacy regulations, both now and in the future. Some of these rules have nationalist interests, like where data can reside. There are some regulations such as:
+ [HIPAA](https://www.hhs.gov/hipaa/index.html) (Health Insurance Portability and Accountability Act)
+ [GDPR](https://gdpr-info.eu/) (General Data Protection Regulation)
These laws are designed to protect privacy. A key element of this regulation is the emphasis on anonymizing data before it is released publicly. Despite the innocent intent of the firm releasing the data, privacy attacks [[2]]() are common. These attacks can be used for re-identification, tracing, or reconstruction by combining existing public information.
Software engineers should adopt a privacy-first approach to complying with these regulations. Privacy by design should not be an afterthought, but a fundamental requirement for building applications that meet users' trust. As expected, governments will evolve these regulations and their enforcement will become more stringent leading to a cat-and-mouse game in play. This is the situation where methods based on solid theoretical underpinnings like differential privacy, and homomorphic encryption among others will become ubiquitous. Firms will get tired of paying fines for privacy violations and invest this money in software engineers, leading to more employment opportunities.
We will remain apolitical for the remainder of this manuscript. This is because I wrote through the lens of intellectual charity, which has the greatest impact on humanity. This is no part of the work that proposes policy positions, and no attempt was made to shape public perception of a politically-charged topic. My goal is to reveal the beauty of mathematics, even though I see myself as a "street-fighting mathematician" who is less formal and jumps steps when writing proofs.
Differential privacy has its roots in cryptography and theoretical computer science. However, I would like to contrast differential privacy with encryption/decryption (cryptography). Both are simple, as differential privacy processing includes an encoder (randomizer) where we add noise and a decoder (analyzer) where we remove some of the noise before performing the statistical calculation. In my opinion, differential privacy encodings are lossy transformations, as we cannot recover the exact original data at the decoder stage. On the contrary, in encryption/decryption (Cryptography), when we decrypt, we recover the exact message that was encrypted. Hence, it is a lossless transformation. Note that we did not consider homomorphic encryption in this analogy, for it is outside the scope of our work.
Differential privacy can be configured in the following settings:
+ Local: Data is randomized on the client before sending off to the server. Local privacy provides stronger privacy guarantees.
+ Central: Data is collected and randomized on the server. Central privacy is easier to abuse in a centralized setting as we trust the server is impartial.
# Mathematical Foundations
The architecture of differential privacy [[1]](), [[10]]()
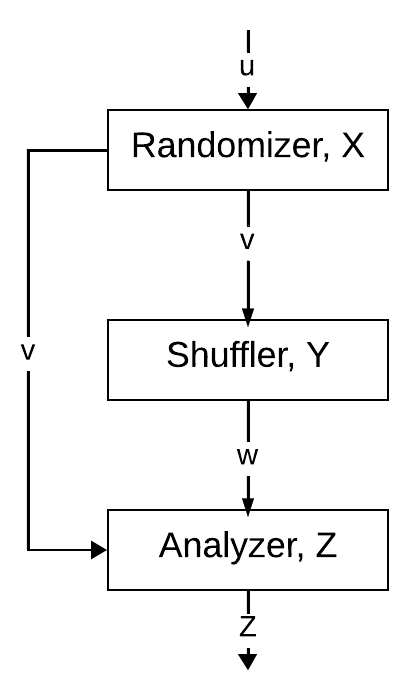
The architecture may be formalized into these phases, which take the form of a pipeline:
+ Randomizer (encoder): takes input from the client device and obtains an intermediary transformed output that is sent as input to the shuffler phase. This adds noise to the input.
+ Shuffler: This is optional in many applications. However, it takes transformed input from the randomizer and does permutation. In some application such as internet traffic, this may prevent privacy attack when the order is used to re-identify and tied a request to an individual (caveat as we assume DNS and other routers does save identifying metadata). We are adding even more noise to the data at this stage.
+ Analyzer (decoder): this phase performs statistical computation on the input from a randomizer or shuffler based on the application. This is where we get insight into the overall data. Ensure that you remove some noise and make meaningful computations needed by the application.
Once, you can transform any two elements of the data, $d, \hat{d}$ using the randomizer, $A$. Every pair of elements, $(d, \hat{d})$, if we have a higher degree of privacy then most element pairs would look similar thereby making it difficult to distinguish. With higher privacy, $Pr(A(d) = y)$ has similar values to $Pr(A(\hat{d}) = y)$. The perfect privacy is when $\xi = 0$, usually most statistical properties are lost, so it is useless for most purposes. No privacy is achieved when $\xi = \infty$. The order of the numerator or denominator does not matter, hence the sign is unimportant $ \pm \xi $.
+ $A: D \rightarrow Y$ (randomizer)
+ ($d, \hat{d}) \in D$ (data) and $y \in Y$ (label)
+ $Pr$: probability
$-\xi \le \ln (\frac{Pr(A(d) = y)}{Pr(A(\hat{d}) = y)}) \le \xi$
Specifying the level of privacy involves setting bound ($\xi, \delta$) [[3]](). This is how we set privacy levels for our application.
$\xi$ is the measure that any two pairs of elements $(d, \hat{d})$ in the data store are similar. This is closely related to semantic cryptography. Privacy guarantees are higher if $\xi$ is closer to 0. Hence, every element in the data store looks the same. This implies that the amount of information gleaned from a single element does not give us information about the remaining data in the data store. Typically, when every item looks the same, then you have maximum privacy. However, in such a situation, we cannot embed useful information in these data. Therefore, we aim to achieve a reasonable level of privacy suitable for the application.
$\delta$ is a measure that represents the loss of information in relation to other items in the database. Smaller values of $\delta$ minimize this loss. This is better described in terms of the attacker's advantage. See multiple cases in examples of probabilistic games in the book [[4]]().
$(Pr_{post}(\hat{X}) - Pr_{pre}(\hat{X})) \le \delta$
The attacker has some information about $X$ which is $\hat{X}$, we want to know how $X$ changes with this newly acquired information from the attacker's perspective. $\delta$ can be referred to as the attacker's advantage based on the latest information about the data.
# Case Studies
This section explores how differential privacy can be used in the industry. The choice is based on applications interesting to the blog author. We begin by providing a principled way for individuals to set privacy bounds ($\xi, \delta$) to prevent privacy violations, which renders our privacy mechanism ineffective. This is followed by a differentially private counting mechanism to estimate the frequency. Finally, we discussed a negative database which is a differential private database mechanism that prevents arbitrary inspection of data.
My writing will explore the following use cases:
+ [Setting Appropriate Values of ($\xi, \delta$) on Application-Specific Case](#optimalNoiseValue)
+ [Privacy-aware Contact Tracing Scheme](#PrivacyAwareContactTracing)
+ [Privacy-aware Video Surveillance System](#PrivacyAwareSurveillanceSystem)
+ [Negative Databases](#NegativeDB)
+ [Frequency Estimation using Differential Privacy](#LearningPrivacyatScale)
### Setting Appropriate Values of ($\xi, \delta$) on Application-Specific Case
The paper [[6]]() released by [Cybernetica AS](https://cyber.ee/) has provided a framework for specifying the values of ($\xi, \delta$) is critical as it can impact the privacy guarantees of the privacy mechanism by computing $\xi$ in relation to $\delta$ which is defined in terms of adversarial attacker advantage with regard to guessing properties of the data. The challenge of setting appropriate values is critical. Setting improper privacy thresholds would severely impact privacy theoretical guarantees for privacy bounds.
Their work presents a formulation of presenting the attacker's goal as a boolean expression over the attributes of the data. Each dimension must be pairwise independent. The paper describes multivariate data. We specify a set of dimensions with a probability, $p$, or a combination of these dimensions. The combinations can be AND-events or OR-events. We provide bounds so that an attacker cannot guess the combination of dimensions. Hence, we add the appropriate amount of noise, $\xi$, defined in terms of a proscribed relative guessing advantage $\delta$.
$\xi = - \ln \frac{(\frac{p}{1-p}) (\frac{1}{\delta+p} - 1)}{R}$
Where $R$ is a scaling value. See paper for exact calculation.
$\xi$ does not have an upper bound and specifying a lower bound is not straightforward. Care must be taken that these bounds are defined in a way that is not affected by scaling. Otherwise, the privacy mechanism is futile. A realistic way to decide the value of $\xi$ based on the prior probability before seeing the data. This is in relation to the posterior probability after seeing the data.
### Privacy-aware Contact Tracing Scheme
One of the ways to minimize infectious disease spread is to identify infected individuals and track them down for isolation. This is until they recover in solitude. [Covid-19](https://en.wikipedia.org/wiki/COVID-19) was an infectious disease and several attempts were made to create a contact-tracing system. However, government regulations meant any system must be privacy-preserving to prevent abuse. Forced isolation would undermine civil liberties and trigger a constitutional crisis if people were forced into solitude. There were several attempts by one by a [Consortium of BigTech firms](https://covid19.apple.com/contacttracing) and a [collaboration of leading European institutions](https://arxiv.org/pdf/2005.12273.pdf).
Most systems use [Bluetooth](https://en.wikipedia.org/wiki/Bluetooth)-like technology for creating peer-to-peer networks. This method uses proximity to infested individuals as a proxy for a covid-19 test to be performed. For this to work, there is a central server with a list of infected individuals that should be anonymous. Each phone can save neighboring pings from the surrounding area and then query a central server to measure if they are close to an infected individual. Contact tracing can also be implemented without a centralized service. This version has data from phones about their covid-19 status and pings so that the phone's status is not broadcast. There needs to be care taken that any broadcast does not expose user privacy. Privacy-enhancing schemes are introduced in these models to preserve identity.
### Privacy-aware Video Surveillance System
[Privid](https://news.mit.edu/2022/privid-security-tool-guarantees-privacy-surveillance-footage-0328) is a privacy-preserving video surveillance system. One may ask why we need surveillance at all if we don't want to recognize the objects depicted in the video? Have we defeated the purpose of video surveillance? Alternatively, does it make sense to follow the maxim "benefits outweigh the risk" where we risk all of our data to the authorities and trust that they won't abuse our information for nefarious intent? Here Benjamin Franklin's words ring true "Those who would give up essential liberty, to purchase a little temporary safety, deserve neither liberty nor safety". Hence, we have justified the need for privacy-enhancing methods based on a robust mathematical framework.
Privacy is achieved by segmenting the video into non-overlapping packets, then structured noise is added to each segment to obscure the identity of the object in the video while preserving the global statistical properties of the streams. Privid can be used for privacy-preserving video surveillance without exposing individuals' privacy to intrusions into their private liberties. Privid can support applications such as face mask monitoring among the population from a video camera, and gait analysis among others. This method allows the identification of masks or gaits without knowing the specific individuals. This allows analysts to query video feeds according to their information-seeking needs.
### Negative Databases
Source code link: https://github.com/kenluck2001/diffprivacy/tree/main/NegativeDB
Interactively querying a traditional database can provide information about stored data. Databases are designed to accomplish this. It is constructed to serve several information-seeking needs. The challenge is how to get aggregate data without exposing individual privacy.
A negative database is a data store that stores only the complement of a record. This prevents insider inspection. This kind of database is suitable for authentication queries. One variant of this negative database that appeared of interest to me is the one based on the boolean SAT problem proposed by the paper [[9]](), which proposes a representation of the data in hard-to-reverse engineering to the actual data based on a 3-SAT problem which is mathematically difficult as NP-hard. The problem is structured so that satisfying a 3-SAT instance proves that a record is in $DB$. For this formulation to succeed, 3-SAT must make it difficult to reverse-engineer a positive record from negative records.
Database inputs are bit strings representing each record. $DB$ is the set representing the actual record stored in the real database, $NDB = U - DB$, where $U$ is the universe, and $NDB$ is the negative database which is the complement of the items saved in the actual $DB$. $DB$ is not physically created as it would expose privacy leaks. Hence, we created $NDB$. $NDB$ has some characteristics as follows:
- In $DB$, inspecting a record incurs a privacy leak
- In $NDB$, inspecting a record does not violate privacy.
When a user saves an item, it stores the complement in the negative database. Thus, the data store contains the complement of items not in the database. By representing a database by its complement, it saves every item not in the database.
Privacy regulations can evolve. A negative database, however, always complies with the strictest privacy laws. There are alternatives such as encryption of the entire database. While it provides privacy, it makes searching almost impossible. Furthermore, a data query restriction policy on a traditional database is unlikely to prevent a determined disgruntled individual with nefarious intentions from arbitrarily inspecting the data.
#### Supported operations
Our implementation supports the following operations:
- Insert
- Delete
- Update is "delete and insert"
#### Cyclic Redundancy Checks
Cyclic redundancy checks is an error-correction code to identify errors using a polynomial divisor while shifting character by character one at a time on a bit string and taking the remainder as a checksum. This scheme identifies or corrects errors. Most error correction schemes have added redundancy to help with error correction and detection.
Communication systems are susceptible to errors. Superfluous strings can be inadvertently introduced in the randomization process for creating hard-to-reverse negative records based on the 3-SAT problem. We can use CRC to handle this case. In most cases, the generator polynomial may identify a burst error. However, our use case will likely have errors due to bit order corruption, rather than burst error.
In our negative database implementation, records are more difficult to reverse-engineer if they are at least 1000 bits long. Hence, I have reversed 1000 bits for the database records and 24 bits for CRC checksums. There are [several standard suggestions for polynomials](http://blog.martincowen.me.uk/choosing-an-optimal-crc-polynomial.html). However, there may be a suboptimal approach to the application's error type. In my case, I have chosen a polynomial hexadecimal value of `6BC0F5`. Our use of CRC has helped to minimize duplicate records and superfluous strings in the negative database.
### Frequency Estimation using Differential Privacy
Source code link: https://github.com/kenluck2001/diffprivacy/tree/main/Privacy-Preserving-Telemetry
This is a large-scale privacy-aware frequency aggregation of event telemetry. During this research, I implemented the following algorithms from the paper [[5]](). They include:
+ $A_{client-HCMS}$ in Algorithm 5.
+ Hadamard count mean sketch HCMS in Algorithm 6.
+ $A_{server}$ in Algorithm 4.
+ Compute Sketch matrix is known as Sketch-HCMS in Algorithm 7.
The paper [[5]]() released by [Apple](https://www.apple.com/) was so influential in my study of privacy that I took the time to derive the formulas in the paper. This information, which I believe the authors omitted due to space constraints.
Their algorithm has a server and client mechanism. The client computes locally and sends intermediary results to the server. The amount of data sent to the server from the client can affect communication costs. The computation done on the server and client can impact the computation cost. The amount of noise added to the client during the encoding phase can impact the amount of privacy afforded and accuracy achieved.
There is a tradeoff between privacy and computation accuracy.
The paper presents two frequency estimation cases:
+ Compute a histogram from a known word distribution.
- This is to count the frequency of a term from a known dictionary of terms.
+ Compute a histogram from an unknown dictionary of words.
- This is to count the frequency of a term from an unknown dictionary of terms.
Hash functions and Hadamard transforms form the core of the algorithm.
Count sketch algorithm: finds frequent data with a near-precise count in a data stream. The client-side algorithm ensures that the privacy mechanism is $\xi$-differentially private.
The data structure on the server to save the privatized data from the client is $M$ ($k x m$) where $m$ is the size of transmitted data from the client to the server, and $k$ is the number of hash functions.
The server-side algorithm averages the count for each $k$ hash function. The hash function should be a set of $k$ 3-wise independent hash functions.
#### K-wise independent hash function family
The privacy algorithm in the paper requires a 3-wise independent hash function to work properly. [Polynomial hash function](https://www.cs.purdue.edu/homes/hmaji/teaching/Fall%202017/lectures/12.pdf) can provide this property.
$H(x) = a_{0} + a_{1}x + a_{2}x^2 + ... + a_{k-1}x^{k-1}$
Where $H(x)$ is a polynomial of $degree \le k$
My approach was to generate a random matrix and extract the vector row-by-row to feed into the hash function, $H(x)$.
#### Hadamard Transforms
Hadamard transforms help to reduce the variance of estimates at the analyzer stage. The Hadamard count sketch algorithm is an improvement over the basic count sketch algorithm with a dense vector instead of a sparse matrix. For more information on Hadamard transformations, consult the following text:
Hadamard Transforms by Sos Agaian, Hakob Sarukhanyan, Karen Egiazarian, Jaakko Astola. SPIE, 2011.
It is desirable to have a shared hash functions family for sampling the hash function for both the client and server. One approach is to create a family of hash functions on the server and send them to the client. However, if we consider communication cost, we have different hash function families with similar distributions and avoid sending huge matrices over the network.
```
// Routine for creating hadamard matric in
// JavaScript using Syvester library
const hadamard = (l) => {
var H = $M([
[1, 1],
[1, -1]
]);
for (let i = 1; i < Math.log2(l); i++) {
var posy = H.augment(H).transpose()
var negy = H.augment(H.x(-1)).transpose()
var hmat = posy.augment(negy)
H = hmat;
}
return H;
}
```
#### Implementation Details
- We observed during implementation that the quality of the solution depends on the hash functions design. As part of this research, I created a custom hash function with superior statistical properties that is near-optimal.
- Negative frequency counts may occur due to negative Hadamard matrix values. Hence, we have to take the absolute and ceiling of the value
- One simplification in my implementation is to use the same random seed for the client and server-side code, so we can sample from the same hash family distribution.
# Acknowledgement
- Thanks to Krystal Maughan for recommending resources to resolve my confusion about cryptographic-related concepts.
- Thanks to the Polyglot reading group for reading privacy papers that got me interested in the subject.
- Thanks to Professor Raija Tuohi for teaching me Cryptography and Probability during my undergraduate days.
- Thanks to the Applied Cryptography reading group I organized, where 7Gate Academy generously provided me with meeting space in their office during off-work hours. The amount of interesting conversation that happened in those sessions was equivalent to studying cryptography at the level of graduate school.
# Conclusion
Privacy laws are taking center stage, which means that only privacy-enhancing methods based on sound mathematical foundations will succeed in the industry. Ignoring the latest trends (fines, ligation) can be imprudent in the face of unending government regulations. Privacy models based on structured mathematical frameworks can future-proof industrial applications under varying legislation.
There is a misconception that differential privacy prevents re-identification attacks. According to the threat model, if the user only has access to the transformed data, privacy can be ensured. However, secondary information can still help re-identify the data. This threat model is very realistic and sufficient in most real-world cases.
Any errors in this manuscript are mine.
# References
- [[1]]() Victor Balcer, Albert Cheu. Separating Local {\&} Shuffled Differential Privacy via Histograms, http://arxiv.org/abs/1911.06879, 2019.
- [[2]]() Cynthia Dwork, Adam Smith, Thomas Steinke, and Jonathan Ullman. 2017. “Exposed! A Survey of Attacks on Private Data.” Annual Review of Statistics and Its Application (2017).
- [[3]]() https://www.johndcook.com/blog/2017/09/20/adding-laplace-or-gaussian-noise-to-database/
- [[4]]() A Graduate Course in Applied Cryptography by Dan Boneh and Victor Shoup. http://toc.cryptobook.us/
- [[5]]() https://docs-assets.developer.apple.com/ml-research/papers/learning-with-privacy-at-scale.pdf
- [[6]]() Peeter Laud, Alisa Pankova. Interpreting Epsilon of Differential Privacy in Terms of Advantage in Guessing or Approximating Sensitive Attributes, https://arxiv.org/abs/1911.12777
- [[7]]() Daniel Kifer, Ashwin Machanavajjhala. Pufferfish: A framework for mathematical privacy definitions, ACM Transactions on Database Systems, Volume 39 Issue 1, pp 1–36, 2014.
- [[8]]() Jaewoo Lee, Chris Clifton. Differential identifiability. In Proceedings of the 18th ACM SIGKDD international conference on Knowledge Discovery and data mining Pages 1041–1049, 2012
- [[9]]() Fernando Esponda, Elena S. Ackley, Paul Helman, Haixia Jia, and Stephanie Forrest. Protecting Data Privacy Through Hard-to-Reverse Negative Databases. In Proceedings of the International Conference on Information Security, 2006.
- [[10]]() Kenneth Odoh, Group-wise K-anonymity meets (ε, δ) Differentially Privacy Scheme. Proceedings of the International World Wide Web Conference (WWW), 2024.
# How to Cite this Article
```
BibTeX Citation
@article{kodoh2022b,
author = {Odoh, Kenneth},
title = {Privacy at your Fingertips},
year = {2022},
note = {https://kenluck2001.github.io/blog_post/privacy_at_your_fingertips.html}
}
```
Footnote:
[Privacy-aware DNS](https://dnsprivacy.org/ietf_dns_privacy_tutorial/), [Oblivious HTTP](https://www.ietf.org/archive/id/draft-thomson-http-oblivious-01.html) can provide privacy on the Internet.
7/18
Please feel free to donate to support my work by clicking