In Sun Tzu's book "The Art of War", he writes, "Attack is the secret of defense; defense is the planning of an attack". A cryptography engineer needs to develop a strong understanding of the subject and be able to break or mitigate a few cryptosystems. This knowledge will enable an individual to build the skill set required to succeed in the cybersecurity industry. Every dual-use technology (Cryptography, Nuclear energy, Artificial Intelligence) with potential military applications has naysayers hyping up an imaginary doomsday event with an existential threat. Motives are difficult to decipher among actors, so we give them the benefit of the doubt. However, these outrageous claims are unfounded and self-serving, for these concerns are overstated and limit intellectual charity.
Security may be an afterthought for many firms. Some managers may even consider security investment a sunk cost for the organization. It is imperative to note that a few cyber security incidents will outweigh the cost savings, as the proposed mitigation and reputation damage can be substantial.
### **Real-Life Impact of this Research**
+ This author has made an exploit for retrieving the full secret key in a variant of Picnic. See the section named [Cryptographic Attack](#cryptoattack).
+ **K Odoh**, Tortoise: An Authenticated Encryption Scheme, [PDF](https://arxiv.org/pdf/2309.05769.pdf), 2023.
+ Blog post titled [Privacy at your fingertips](https://kenluck2001.github.io/blog_post/privacy_at_your_fingertips.html)
# Table of Contents
+ [Introduction](#introduction)
+ [Algorithm implementations](#algorithm-implementations)
+ [Discussion](#discussion)
+ [Cryptographic Attack](#cryptoattack)
+ [Future Work](#futurework)
+ [Acknowledgements](#acknowledgments)
+ [Conclusions](#conclusion)
+ [References](#references)
# Introduction
Real-world cryptography protocols are broken in multiple ways. This precarious situation provides an opportunity for a determined ethical hacker to uncover the internet's betterment. On the other hand, it also provides an opportunity for black hat hackers to damage their prey. Developing cybersecurity skills can help build a safer internet. Most armies were not created to win wars, but to make attacks prohibitive for the enemy. This analogy fits the selling point for cryptographic schemes.
##### Notes:
- Our work is neither affected by [Canadian Export Control](https://www.international.gc.ca/controls-controles/export-exportation/crypto/FAQ2011.aspx?lang=en) nor [US Arms Export Control Act](https://en.m.wikipedia.org/wiki/Arms_Export_Control_Act), as it is already in public domain and not subject to [arms trafficking export controls](https://en.m.wikipedia.org/wiki/Export_of_cryptography).
- We strive to be beyond ethical (moral) and discourage bad actors from gaining insight from our work. Every black hat hacker deserves a punishment to the fullest extent permitted by law.
- Every source code is the author's original work. The accompanying software is done in good faith and makes no claim about the correctness of the solution to the extent possible under the [MIT license](https://opensource.org/license/mit/).
- This is intended to be a living document. See it as a research manifesto.
- Repo: https://github.com/kenluck2001/cipherResearch
Understanding the fundamentals can help discover out-of-the-box vulnerabilities before a well-funded bad actor beats us to it. Anecdotal evidence suggests that exploiting a known attack vector may not be feasible due to limited technical mastery of the subject. A gulf in execution could impact the transfer of theoretical insights from theory to practice. Practicality entails simplifying (abstracting) the real-world within reasonable constraints to achieve a proof-of-concept. For-profit certification has some utility, but security is a multi-headed hydra, so training individuals in a gamified system can be relevant for the basics, but will not help identify the rare vulnerabilities which would likely yield the highest utility for bad actors. We recommend solving the [cryptography puzzles](https://cryptopals.com/).
# Algorithm implementations
Here is a popular cliché, "Don't roll out your own cryptosystem". The original advice was to prevent security incidents due to poor cryptography implementation and understanding. A second school of thought views the advice as an attempt to entrench elite knowledge. Autodidacts learn by building from scratch, as every expert was once a novice. Based on personal experience, I can say that Software Engineers at top-notch firms also experience doubts. In most cases in the real world, "Don't roll out your own cryptosystem, but build protocols using well-tested ciphers."
What happens if you protect your national interests in the face of crippling sanctions? In such a hypothetical situation, cryptographic software may no longer be available. Here is one contrived use case for learning to roll out your crypto. As a matter of emphasis, this idea does not represent the author's intentions, either in the future, present, or past.
The Cryptosystems algorithm created for experiments is as follows:
| S/N | Algorithms | Source Codes |
| :--- | :----: | ---: |
| 1 | Data Encryption Standard [[1]]()|[des.py](https://github.com/kenluck2001/cipherResearch/blob/main/src/des.py) |
| 2 | Advanced Encryption Standard [[2]]()|[aes.py](https://github.com/kenluck2001/cipherResearch/blob/main/src/aes.py) |
| 3 | Ascon (Lightweight Cryptography) [[3]]()|[ascon.py](https://github.com/kenluck2001/cipherResearch/blob/main/src/ascon.py) |
| 4 | Picnic (Post-Quantum Signature) [[5]]()|[picnic.py](https://github.com/kenluck2001/cipherResearch/blob/main/src/picnic.py) |
| 5 | FrodoPKE [[6]]()|[frodopke.py](https://github.com/kenluck2001/cipherResearch/blob/main/src/frodopke.py) |
| 6 | Deoxys [[4]]()|[deoxys](https://github.com/kenluck2001/cipherResearch/tree/main/src/deoxys) |
| 7 | Post-Quantum Lattice-based Blind Signature [[7]]() |[signature](https://github.com/kenluck2001/miscellaneous/tree/master/src/auth) |
# Discussion
During this investigation, I made the following observations.
##### Data Encryption Standard, DES [[1]]()
| 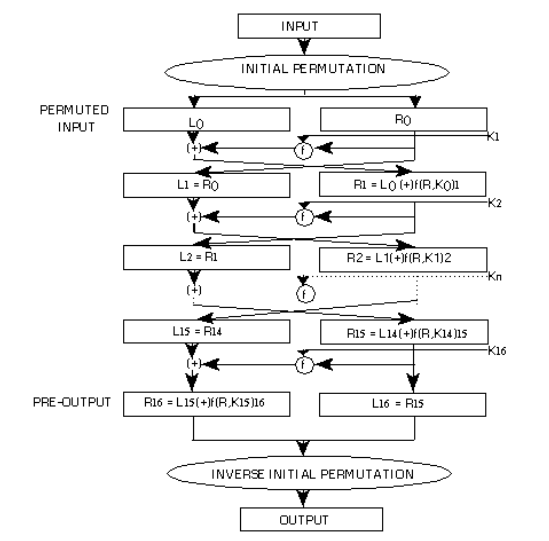 |
|:--:|
| DES Cipher (encryption scheme) [[1]]() |
- The block size is context-specific as we can use (4, 6, 8) bits per block as required.
- DES reserves 1 byte for error recovery. The scheme for error recovery is not clear to me. Observing the algorithm, it's probably in the method `'E BIT-SELECTION TABLE'` where we increase the 48 bits to provide bit pattern arrangement so that errors can be detected.
- In my DES implementation, I settled for 4 bits to avoid fractional bytes in the key schedule scheme in the `'ObtainKeyListParameters'` method. At this moment, it is unclear if I need a left-shift or a circular-left-shift. In my opinion, a pure left-shift may lead to entropy loss as we iterate for 16 rounds. Hence, I have used a circular left-shift, as it may be more secure and could enhance the [diffusion and confusion](https://en.wikipedia.org/wiki/Confusion_and_diffusion) properties of the cipher.
- Moving beyond 16 rounds is a waste of computing because if you left-circular-shift 4 bits at a time, after multiple rounds, you are back to the original block representation and doing repeated futile work.
- I did not consider the initial and inverse initial permutation transformations in my implementation. At this moment, I am not sure how this change impacts the overall cipher's security.
##### Advanced Encryption Standard, AES [[2]]()
- Permutation is the process of increasing entropy in the data representation.
- Key expansion schemes allow users to utilize small-sized keys and get the security benefits of using a large-sized key.
- Larger-sized key (256 bits and above) in AES is "[Military Grade Cryptography](https://www.howtogeek.com/445096/what-does-military-grade-encryption-mean/)", even though the original message blocks are 128 bits.
##### Ascon [[3]]()
| 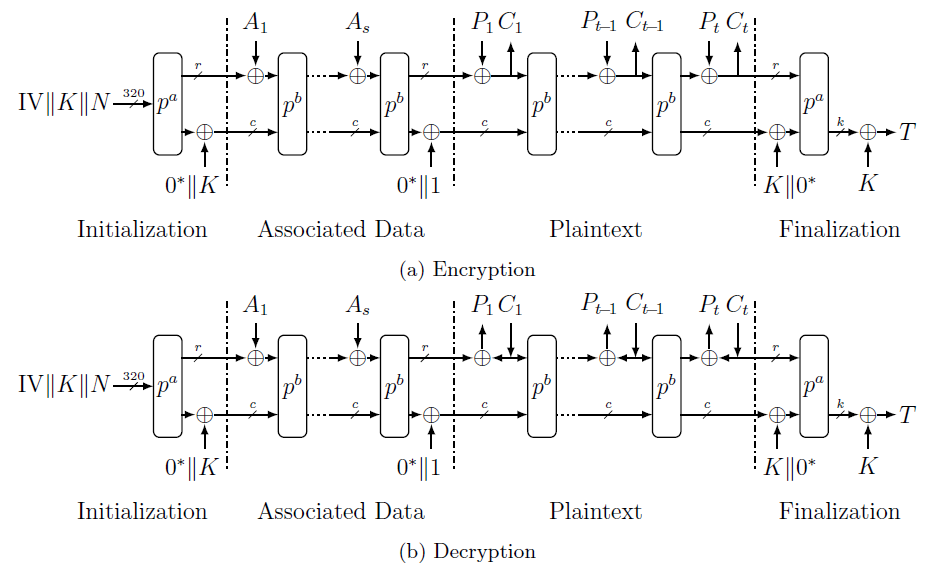 |
|:--:|
| ASCON Cipher [[3]]() |
ASCON is a lightweight authenticated encryption scheme. The padding is multiples of the `r-bits` message block. When properly implemented, ECB and CBC modes may not be needed. The initialization vector is auto-derived and not user-supplied. It also uses nonce to prevent replay attacks. The associated data is used to update the state. Another use-case for associated data is to capture metadata about the plaintext (ancillary information about the plaintext) that is uniquely identifiable. It employs S-Box to resist differential cryptoanalysis and facilitate the future integration of schemes for side-channel attack mitigation. Decryption should return data only after signature verification passes.
The permutation routine uses the Hadamard product for binary, which I approximated as an AND operation.
##### Picnic [[5]]()
Picnic is a post-quantum cryptographic signature system. This is a public key cryptography system, where the user creates a pair of private and public keys using the KDB++ protocol. This is done to create an irrefutable signature on a document during the signing phase. The signature is based on the user's private key and document digest. The signature can be used to authenticate the document owner by his private key, which is only known by him. However, during the verification phase, the user wants to know if the document is signed by the party it claims to be, thereby preventing forgeries. In this phase, the user uses the signer's public key to ensure that the signature can be recreated. This signature matches the exact signature created at the time of signing. This would require a description of the following concepts in no particular order. They include: [Zero-knowledge proof](https://en.wikipedia.org/wiki/Zero-knowledge_proof), [Secure multi-party computation](https://en.wikipedia.org/wiki/Secure_multi-party_computation), [Commitment schemes](https://en.wikipedia.org/wiki/Commitment_scheme), and, Circuit decomposition.
Let us describe the concept of Zero-knowledge proof with the analogy of a teacher and student. The teacher wants to know if the student knows his real age and wants to validate the student's age without the student saying his/her age out loud. The teacher creates a set of challenges and sends them to the pupil several times. The teacher can validate that the student knows his/her age without knowing the exact student's age. The teacher can verify the secret (age) knowledge by grading the student's response to his challenge, then checking for consistency in the pupil's answers. For the analogy, we may limit the challenge to a combination of a few mathematical operations of the student's age. The teacher feels confident that the student knows his/her age if he creates many challenges and if there is consistency in the student's response that is beyond random chance (>=50%). The teacher has only verified the student's age without actually knowing it.
The above description of zero-knowledge proof is interactive and requires multiple round trips. Furthermore, due to the interactive nature between the prover (student) and the verifier (teacher), there is a chance that transcripts can be obtained and used for replay attacks. Hence, we need to allow the student and teacher to role-play the change and response scenario on their own. Simulating a multiparty computation circuit is used by both parties to perform this self-thinking. The original zero-knowledge proof is interactive and hence converted to a non-interactive form by [Fiat-Shamir transformation](https://en.wikipedia.org/wiki/Fiat%E2%80%93Shamir_heuristic) and UR transformation, leading to a minimized round trips compared to interactive forms.
Each party runs a challenge/response flow. It is like talking to yourself to prevent your conversation transcript from being eavesdropped by a third party. By decomposing circuits, multi-party computation becomes more efficient. Multiparty computation requires multiple parties to cooperate to complete a task. Let's say $x$ is the data to be computed. The $x$ is split into shares $x_1, x_2, x_3$ and $x = x_1 + x_2 + x_3$, in the case of 3 parties in the mix. We have each party having $x_i$ where $i$ is the index of the number of parties. In our case, we can retain the privacy of $x$ at most if only two shares are exposed. If the 3 shares are exposed, it is trivial to get the secret $x$ where $x = x_1 + x_2 + x_3$. (2, 3) Circuit decomposition is a protocol that provides 2=privacy when there are 3 players in the circuit. Even if two players reveal their shares, privacy is not compromised.
In my implementation of Picnic, I used only the Fiat-Shamir transformation. My Python installation does not use the [SHAKE](https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf) hash algorithms which provide a variable output from the algorithm unlike SHA1, MD5, SHA224, SHA512 which has a constant output. Due to the change, I had to modify the challenge rounds to $T$ where the length of the challenge is upper bounded by $\frac{T}{2}$. I ignored serialization to string as it is easy to integrate into real production settings, unlike experiment prototypes based on my research.
The KDB++ scheme was utilized to create public and private keys. I used AES instead of LowMC, despite using a higher number of multiplications in the hardware. However, the LowMC cipher has required a minimal number of multiplications in its operations. It has been used for encryption flow during signing and decryption flow during verification.
There is a problem in the specification, where the seeds created in the signing phase cannot be easily retrieved in the verification step. Hence, I modified my implementation to allow for seed retrieval. My exploit involved the release of the third player's shares at the end of the signing phase. More details on my vulnerability will be included in an upcoming section called "Cryptography Attack" in this blog.
Unfortunately, for unknown reasons, I am unable to do so as debugging is ongoing. I suspect without concrete evidence may be due to using a Sbox that may not be invertible. I could not recreate the challenge created during signing during verification.
##### FrodoPKE [[6]]()
Current cryptography schemes are based on integer factorization and discrete logarithms. Unfortunately, quantum computers can solve these foundational problems easily.
Key encapsulation mechanisms (KEM) and public key encryption (PKE) schemes are the most common methods of post-quantum cryptography. KEM is an ideal key exchange protocol for creating shared keys between communication participants. PKE allows the creation of public and private keys for encrypting and decrypting messages. It is easier to manage keys in a PKE than in secret-key cryptography. One potential advantage of KEM is it can help us create ephemeral keys for communication and achieve [forward secrecy](https://crypto.stackexchange.com/questions/81745/what-does-perfect-mean-within-perfect-forward-secrecy-and-why-do-some-cryptograp).
[NIST](https://csrc.nist.gov/Projects/post-quantum-cryptography/selected-algorithms-2022) has favored lattice-encryption cryptography. Most lattice-based algorithms are based on `"Learning with errors"` (LWE). The problem is summarized in [Short Vector Problem](https://cseweb.ucsd.edu/~daniele/LatticeLinks/SVP.html) and [Shortest Independent Vector Problem](http://web.stanford.edu/class/cs354/scribe/lecture13.pdf).
LWE recovers a secret vector, $s \in {Z_q}^n$. Here is a description based on the [book](https://eprint.iacr.org/2015/938.pdf).
Alice creates the following:
- creates $e \in {Z_q}^{1 \times m}$
- secret vector: $s \in {Z_q}^n$
- public key: $A \in {Z_q}^{n \times m}$, ${b}^t = {s}^t A + {e}^t$
Bob sent the following to Alice:
- creates $x \in \left({0,1}\right)^{m}$
- create $u, \hat{u}$ respectively.
+ $u = Ax$
+ $\hat{u} = {b}^t x + bit \frac{q}{2}$
On receipt, Alice decodes $\hat{u} - {s}^t u \approx bit \frac{q}{2}$
Because we created an underspecified simultaneous equation without providing a y-intercept, the expected runtime will be exponential. Hence, it cannot be solved by Gaussian elimination.
I like FrodoPKE because it does not use polynomials. These polynomials can be difficult to implement because they may have specific structures that make estimating roots difficult. FrodoPKE uses a conservative approach to ensure its security. With suitable parametrization, we can achieve security levels 1, 3, and 5. Despite my implementation challenges due to Endian mismatches. FrodoPKE provides schemes for key encapsulation and public key encryption. As part of my research, I have implemented a public key encryption scheme using the FrodoPKE cipher
##### Deoxys [[4]]()
Deoxys is an authenticated encryption scheme, which was a winning submission to the [CAESAR](https://en.wikipedia.org/wiki/CAESAR_Competition) competition in the `"defense in depth"` category. There are two modes of the algorithm, nonce-respecting and non-misuse-resistance. In my opinion, it isn't a novel cipher, but a principled method for strengthening existing ciphers. There are several ways to harden a cipher, including the [Triple DES](https://en.wikipedia.org/wiki/Triple_DES) mechanism and alternating ciphers in a [CBC](https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation)-like mode. Deoxys takes a different approach to harden uses AES as a routine and enhances it by applying several checksums, careful padding, and other non-linear operations, thereby making it resilient to replay attacks even when nonce are reused. In addition, it also makes the cipher invulnerable to birthday-bound attacks. Since most published ciphers have weaknesses, designers do not need to start from scratch. Instead, they can patch existing ciphers and benefit from their proven security and robustness.
Note: this scheme must use a tewakable block cipher, otherwise, we just have ECB especially without padding. My current implementation does not use a tweakable cipher.
##### Mitigating Timing Attacks
A principled way of performing constant-time operations could be the holy grail for implementing real-world ciphers.
- Use tables to speed up computation and minimize branching (for number representations (binary, decimal).
- All permutation functions in DES should have equal length, which may require some padding as we permutate 32, 48, and 64 bits in varying contexts.
- Is a double $for-loop$ of length, $n$ equivalent to a single $for-loop$ of length, $2n$ in terms of timing?
- The number of rounds is not considered a timing leak. Each round step may be unrolled in a single operation, if there is an impact on timing in $for-loop$ in each round.
- Timing behaviors may vary across many processors. Cross-platform support would depend on building a small set of generalizable categorizations across processors.
- Avoid flighting the timing-specific mitigations, as branching may provide an attack vector.
##### Practical Considerations
Message and key are represented in bits in the specification. It should not be confused with storage space in actual memory.
- Utilize precise padding between number representations to prevent fractional bytes at (word, byte) boundaries.
- When implementing a cipher that interacts with the real world. Conforming to the standard avoids deviations that result in undecipherable messages. Understanding the intricacies of the specifications is imperative, so the most effective approach is to validate your solution with the gold standard (cipher, plaintext, key).
- We can detect ciphertexts in ECB mode more easily in transmission since we have every nonoverlapping 16-byte segment until the end of the message, and check for collisions.
- [PKC#7](https://datatracker.ietf.org/doc/html/rfc2315) padding scheme is a common standard for addressing variable-sized messages, by adding many characters to make every message block equal in length. It appends `/x04` to extend the string length.
- Combination of secure ciphers chained in [cipher block chaining](https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation) (CBC)-like manner where different ciphers are utilized to encrypt alternating blocks, thereby improving the hybrid cipher's security.
- Use a combination of different keys in a structure similar to [Triple DES](https://en.wikipedia.org/wiki/Triple_DES), but use a more secure cipher. This configuration can create a more secure hybrid cipher.
- No matter how effective the cryptographic scheme is in practice. There is always a chance of compulsion by authorities in the form of [rubber-hose cryptanalysis](https://en.wikipedia.org/wiki/Rubber-hose_cryptanalysis).
- Debugging a program that has an undocumented mixup of (big-endian and little-endian) bit order can be very tricky. In reality, endianness can be described as a representation of bits in memory address locations. There are two options: bytes are either represented from left to right or from right to left. I have spent a few days investigating a bug due to a mismatch of endianness, especially when it is not documented. There are a few remedies, but varying word sizes and other variables can make triaging a nightmare. Unfortunately, the small details take the most debugging time.
- As a result of my lack of knowledge in coding theory and error control codes, I lack the needed background. For example, Classical McEliece uses Goppa code. I have issues understanding the generator matrix, the rationale for the row-echelon form of matrix in systematic form, and other ideas in coding theory that can help me understand Reed Solomon codes, turbo codes and other error correction schemes to allow for implementation simplification.
# Cryptographic Attack
My attack on the picnic scheme and the author's response are covered here. Here are the details.
Step 5 on page 12 of the [attached spec](https://github.com/kenluck2001/cipherResearch/blob/main/references/spec-v3.0-picnic.pdf) has a risk of leaking the secret key during the verification process
This is a specific flow in Figure 1.
|  |
|:--:|
| Figure 1: Picnic signature scheme [[5]]() |
In Figure 1, we have highlighted the screenshot in Figure 1 with labels (`"A"` and `"B"`) depicting $view[t][2].iShare$ should not be shared at all because, in the MPC circuit in the verification flow, we only use two parties. Therefore, releasing the third share from the signing flow will release the secret key. The secret has only undergone a linear transformation as shown below
\begin{equation}
x[2] = sk ⊕ x[0] ⊕ x[1]
\end{equation}
The secret key is not transformed by a non-linear transformation, making it vulnerable to multiple attacks.
The secret key, sk, is constant for every T round as described in the specs. We can recreate two parties ($v[0], v[1]$) and we can recover the secret key in the verification phase
\begin{equation}
sk = x[2] ⊕ v[0] ⊕ v[1]
\end{equation}
My suggestion is to fix the issue and ensure that all the seeds can be recovered, because in the present form of step 5 of signing. If the first challenge string is 1, we cannot recover `seeds[0]`, but with this modification.
This specific flow for labels (`"A"` and `"B"`) as shown in Figure 1, should be replaced with $view[t][0].iShare$ and $view[t][1].iShare$ respectively.
In essence, do not share anything about the third player from the signing process, in the verification as we will recreate it on the verifier alone.
##### Response from the algorithm author
"""
In each of the T parallel repetitions, new independent random shares are chosen. The key is the same, but three fresh shares are chosen, only two of which are revealed. The attack you’re proposing might work if the same shares were used in more than one parallel repetition, but that’s not what Picnic does.
You should be able to try out your proposed attack using the Picnic reference implementation.
"""
# Future Work
These are topics I intend to explore in the coming years. They include:
- Constant-time cryptography
- Lightweight cryptography
- Post-quantum cryptography
- [Zero-Knowledge Proofs](https://en.wikipedia.org/wiki/Zero-knowledge_proof)
- [Homomorphic Encryption](https://en.wikipedia.org/wiki/Homomorphic_encryption),
- [Secure Multi-Party Computation](https://en.wikipedia.org/wiki/Secure_multi-party_computation)
- [Error correction code](https://en.wikipedia.org/wiki/Error_correction_code)
# Acknowledgement
- Thanks to Krystal Maughan for recommending resources for understanding cryptographic-related concepts.
- Thanks to Professor Raija Tuohi for teaching me Cryptography and Probability during my undergraduate days.
# Conclusions
Finally, this blog post is educational. Due to the vast nature of cybersecurity, one would require more supplementary material and significant domain knowledge to succeed in [Bug Bounty Programs](https://en.wikipedia.org/wiki/Bug_bounty_program) or to win [CTF Competitions](https://en.wikipedia.org/wiki/Capture_the_flag_(cybersecurity)).
# References
- [[1]]() [Data Encryption Standard](https://github.com/kenluck2001/cipherResearch/blob/main/references/FIPS%2046-2%20-%20(DES)%2C%20Data%20Encryption%20Standard.pdf).
- [[2]]() [Advanced Encryption Standard](https://github.com/kenluck2001/cipherResearch/blob/main/references/NIST.FIPS.197.pdf).
- [[3]]() [Ascon v1.2](https://github.com/kenluck2001/cipherResearch/blob/main/references/asconv12.pdf)
- [[4]]() [Deoxys v1.41](https://github.com/kenluck2001/cipherResearch/blob/main/references/deoxysv141.pdf)
- [[5]]() [Picnic](https://github.com/kenluck2001/cipherResearch/blob/main/references/spec-v3.0-picnic.pdf)
- [[6]]() [FrodoPKE](https://github.com/kenluck2001/cipherResearch/blob/main/references/FrodoKEM-specification-20210604.pdf)
- [[7]]() [Lattice-based Blind Signatures](https://eprint.iacr.org/2008/322)
# How to Cite this Article
```
BibTeX Citation
@article{kodoh2023a,
author = {Odoh, Kenneth},
title = { Probing Real-World Cryptosystems },
year = {2023},
note = {https://kenluck2001.github.io/blog_post/probing_real-world_cryptosystems.html}
}
```
6/18
Please feel free to donate to support my work by clicking