This blog post is the culmination of several technical talks given at the Python Conference (Singapore) in 2018 and a meetup session held in Vancouver titled “Tracking the Tracker: Time Series Analysis in Python from first principles”. The slides and video recordings can be found in [slides](https://www.slideshare.net/kenluck2001/tracking-the-tracker-time-series-analysis-in-python-from-first-principles-101506045), [video_1](https://youtu.be/jGiHxHt1q6A), and [video_2](https://youtu.be/cTeTGHI6vBU). Python programming language is widely used for scientific computation due to the proliferation of third-party packages such as NumPy [[04]](), Scipy [[J+01]](), and Pandas [[12]]() among others. The availability of extensive documentation for these packages and many built-in package managers (pip [[08]]() and easy\_install [[04]]()) for stress-free installation of these libraries. This situation has given rise to wider adoption of Python programming in diverse domains. Feel free to also check my related blog on [anomaly detection on multivariate time series](https://kenluck2001.github.io/blog_post/real-time_anomaly_detection_for_multivariate_data_stream.html).
Time series analysis is a ubiquitous problem that occurs in many interdisciplinary domains such as finance, social sciences, and engineering. There is an inherent need for an easy-to-use time-series library that serves the needs of multiple users. PySmooth was released as an open-source library to promote mass adoption with the least restriction on usage, thereby ensuring that the source code is accessible to practitioners, students, and researchers. Why put oneself through the stress of writing a brand-new software library, when there are existing alternatives in the wild? This is not exactly the case as our approach is unique because to the best of our knowledge the majority of existing time series analysis libraries tend to lack a state-space formulation. However, PySmooth is unique in solving the general time series problem by reducing it to a state-space formulation.
The software was built with a philosophy that encourages pedagogy by designing an application programming interface (API) that is easy for novice users to use the package in their work with minimal training. The usage of the software shouldn't impose a significant cognitive burden on the user. Furthermore, the API should provide a trade-off between educating the user on the logical functionality of the library and managing the complexity of the software design. Some users are interested in using the library to solve the problem at hand. A different set of users are curious about perusing the internals of the library to refactor the library. PySmooth was built to meet the expectations of a diverse set of users.
This paper gives a presentation of the software architecture and algorithms used in the PySmooth library. The fundamental architecture of PySmooth is suited to real-time analysis of time series data. Under the hood, PySmooth uses NumPy for all the matrix operations.
Our contributions consist of the following:
- Creation of a novel online ARIMA algorithm based on RLS [[WZ91]]().
- [Comprehensive proof](https://www.geogebra.org/m/t7Gj6Vv3) of Kalman filter equations from first principles. Thanks to Dr. Eugene for the creative charts.
- Providing software implementation in an easy-to-use package [[Odo17]]().
This paper is organized as follows. In the Literature Review section, we present a review of major milestones in the development of the field of time series analysis. In the Implementation section, we describe the algorithms in PySmooth and give justifications for the software design. In the Evaluation section, we provide empirical testing of the algorithms in the PySmooth [[Odo17]]() Library. We conclude the paper with a reflection on the research presented in the paper and a proposal for further research.
### Literature Review
Every activity that requires planning for the future tends to require some form of forecasting of future events. Forecasting is an invaluable aspect of planning activities within organizations. This can be used for resource allocation, as gridlocks can be avoided once we know what to expect in the future. The reliability of the estimation is of high importance due to the cost of a failed prediction. Unreliable forecasting is tantamount to inefficient planning for the future. Accurate forecasting is essential for these systems to be deployed in production. Ideally, the time series analysis library should be adaptive, self-healing, and self-correcting to learn from the data. Additionally, the need for real-time predictions exacerbates the problem of reliability. This calls for a method that can make quick predictions and make corrections to future estimations as more data arrive, even in the presence of concept drift [[WSK10]]().
Popular time series analysis projects like Facebook's prophet [[TL17]]() allow for a man-in-the-loop adjustment and review. In contrast, we take a different approach by automatically doing the prediction with a self-healing method, thereby avoiding a man-in-the-loop. This allows for self-correction in changing distributions of the stream. Humans need to have domain expertise to be useful in the prediction loop. We want to save the cost of training a human and avoid some preconceived biases that are inherent in humans. The models are largely interpretable and explainable, so we have fewer problems in that context. These design decisions mean that the library can be used out of the box by practitioners for some non-trivial tasks within reason. This paper proposes a number of time series algorithms that are flexible and can predict even when concepts drift. Prophet also has a break change detection with a scheme that looks like a simplified Multivariate adaptive regression spline (MARS) in terms of the piecewise regression, which we don’t support. The scale cannot be compared as it is battle-tested. Ours is a poor-man time-series library.
A time-series problem can be formulated as a curve-fitting procedure that captures the time dependence on the stream. It is possible to decompose every time series into a trend, seasonality, and holiday component [[HP90]].mponent [[HP90]]. The ARIMA models which were developed by Box and Jenkins [[BJ90]]() have been utilized in linear time series modeling. However, the average user would have difficulty obtaining the appropriate parameter values for the order of difference, autoregressive component, and seasonality difference. Muth [[Mut60]]() laid the foundation for exponential smoothing by showing that it provides optimal estimates using random walks with some noise. Further works were done to provide a statistical framework for exponential smoothing leading to the creation of linear models, [[BJ76]](), [[Rob82]](). Unfortunately, this does apply to nonlinear models. Yule postulated a formulation of time series as a realization of a stochastic process [[Yul27]]().
Kalman filter is a recursive algorithm for incrementally recomputing forecasts based on past data [[Kal60]](). This is ideal for one-step prediction, and it is not so difficult to extend to the case of multi-steps prediction. There are theoretical estimations of the multi-step look-ahead forecast error [[GK92]]() with bounded guarantees. Due to the popularity of linear models, there is a movement toward solving nonlinear models by linearizing a nonlinear model into a linear model [[FZ98]]() with accuracy to higher orders such as the Extended Kalman filter which is a linearization by Taylor series.
\begin{equation}
\label{add}
Y_t = V_t + S_t + H_t + \xi_t, \quad t = 1,...,n
\end{equation}
where $V_t$ is the trend in the data, $S_t$ is seasonality in the data, $H_t$ is the holiday in the data, and $\xi_t$ is an error. The trend, $V_t$, is a varying component, and seasonality, $S_t$, is the cyclic component and the holiday component helps in modeling discontinuous time series as seen in Equation \ref{mult}.
The time series can be multiplicative
\begin{equation}
\label{mult}
Y_t = V_t * S_t * H_t * \xi_t, \quad t = 1,...,n
\end{equation}
From this Equation \ref{mult}, we can take logs and ignore the scalar multiplier, thereby giving rise to Equation \ref{add}.
Neural networks have been used for time series applications [[PP14], [Mal+17], [Dor96], [LB98]]() as a consequence of the universal approximation theorem [[Cyb89], [Hor91]](). Due to the ability to predict sequences, recurrent neural networks (RNN) [[JM99]]() and long short-term memories (LSTM) [[HS97]]() are suited for time series.
### Implementation
PySmooth is designed as a time series analysis library to support real-time series analysis for time series data.
##### Recursive Linear Regression
The Matrix Inversion Lemma RLS, version 1 of page 89 in the paper [[WZ91]]() is the version used in the implementation.
- Initialize model at time, $t$, and update as new data arrives at time, $t+1$. During inference, prediction can be done by $y = \theta_{t} * x_t$
- During training time, at later time, $t+1$, we receive $x_{t+1}$, $y_{t+1}$, and estimate $\theta_{t+1}$ in an incremental manner. Using Matrix Inversion Lemma RLS, version 1,
- At time, $t+1$, estimate residual, $\rho_{t+1} = y_{t+1} - x^T_{t+1}\hat{\theta_{t}}$.
- Using Sherman and Morrison formula to get inverse of coefficient in a form that can be used for future optimized operation.
$P_{t+1} = P_t \left( \mathbb{I} - \frac{ x_{t+1} \times x^T_{t+1} P_{t} } { 1 + x^T_{t+1} P_{t} x_{t+1} } \right) $
- Update parameter, $\hat{\theta_{t+1}} = \hat{\theta_{t}} + P_{t+1} x_{t+1} \rho_{t+1}$
- Repeat the process as new data arrives.
```
import numpy as np
from utils import OnlineLinearRegression
olr = OnlineLinearRegression()
y = np.random.rand(1,5)
x = np.random.rand(1,15)
olr.update(x, y)
print olr.getA( ) # $\theta$ matrix
print olr.getB( ) # bias vector
y = np.random.rand(1,5)
x = np.random.rand(1,15)
olr.update(x, y)
print olr.getA( ) # $\theta$ matrix
print olr.getB( ) # bias vector
```
##### Time Difference
The RLS routine described in this Subsection is used for mapping input to output in Equations 2.1 and 2.2 of the paper [[WB95]](). The mathematical representation of the time difference model is shown in Equation \ref{time_diff}.
\begin{equation}
\label{time_diff}
y_t = \theta_1 * y_{t-1} + \theta_2 * y_{t-2} + \theta_3 * y_{t-3} + ... + \theta_p * y_{t-p}, \quad t = 1,...,n
\end{equation}
where $y_t$ is the current value at time, $n$ is the number of samples, $t$, and $\theta_i$ is the weights of current at offset, $i$ where $i > 0$ and $i \leq p$ where are fitting a regression on the current data at time $t$ and a history of $p$ data points. This is also known as the pth-order difference equation.
```
import numpy as np
from TimeDifference import TimeDifference
X = np.random.rand(200,4)
d = 5 #time lag
tdObj = TimeDifference(d)
#train a model
tdObj.train( X )
#predict on lag
y = np.random.rand(5,4)
ypred = tdObj.predict ( y )
print ypred
```
##### Online ARIMA
Autoregressive processes (AR) and moving average processes (MA) were introduced by Yule in paper [[Yul27]](). This is also used to make the time difference model described in this Subsection operate in an incremental model, as in equation 1.2.1 on page 7 of the paper [[Hami94]](). Both AR and MA processes in Equations \ref{maprocess} and \ref{arprocess} respectively make use of the RLS to perform the process of performing the ARIMA model incrementally.
ARIMA is an appropriate linear model for time series forecasting due to its flexibility. Estimating the parameters in a batch manner is not suitable for real-time prediction. The combination of MA and AR processes which is fitting regression of the past observation and residual with some biases gives rise to the ARMA process as shown in Equation \ref{armaprocess}. A transformation is applied to the ARMA process to get an ARIMA process as shown in Equation \ref{arimaprocess}. RLS implementation from the Subsection on Recursive Linear Regression was used to make the ARIMA model work incrementally.
The closest parallel work is [[Liu+16]](), which involves relaxation of the noise terms in the mathematical formulation. Their model pretended that noise terms don’t exist, which is trading off the noise for computational efficiency. In our case, we have taken a superior path by modeling both the noise term and performing real-time computational in a computationally efficient manner. We have modeled the noise of a bias term as part of a regression fitting scheme. The model uses the Sherman and Morrison formula to update the parameters incrementally. Our approach is built to be based on modular routines as such the base model can be reused in other online algorithms. Using the principles of compositionality, we have decomposed the model into several smaller models and described the underlying routines.
\begin{equation}
\label{maprocess}
Y_t = \mu + \rho_t + \theta_1 \rho_{t-1} + \theta_2 \rho_{t-2} + ... + \theta_q \rho_{t-q}, \quad t = 1,...,n
\end{equation}
where $Y_t$ is the current data point, $\mu$ is the mean or trend, $\rho$ is the residual error at the time, $t$. We are using the history of residual errors to capture the dynamics of the system, $\theta_i$ is the regression coefficient were $0 < i \leq q$. This is the qth-order moving average process.
\begin{equation}
\label{arprocess}
Y_t = c + \rho_t + \theta_1 * Y_{t-1} + \theta_2 * Y_{t-2} + ... + \theta_q * Y_{t-q}, \quad t = 1,...,n
\end{equation}
Where $Y_t$ is the current data point, $c$ is the bias, $\rho$ is the residual error at the time, $t$. We are using the history of past observations to capture the dynamics of the system, $\theta_i$ is the regression coefficients where $0 \leq i$$ \leq q$. This is the qth-order autoregressive process.
\begin{equation}
\label{armaprocess}
Y_t = c + \theta_1 Y_{t-1} + \theta_2 Y_{t-2} + ... + \theta_p Y_{t-p} + \rho_t + \alpha_1 \rho_{t-1} + \alpha_2 \rho_{t-2} + ... + \alpha_q \rho_{t-q}, \quad t = 1,...,n
\end{equation}
where $Y_t$ is the current data point, $c$ is the bias, $\rho$ is the residual error at the time, $t$. We are using the history of past observations to capture the dynamics of the system, $\theta_i$ is the regression coefficients where $0 \leq i$$ \leq p$ on the history data, and $\alpha_i$ are the regression coefficients were $0 \leq i$$ \leq q$ on the history residuals. This is the ARMA process.
ARMA is suitable for modeling the behavior of noisy dynamic systems. ARMA assumes a linear relationship in stationary data. ARIMA improves ARMA by introducing a differentiating scheme that allows for the analysis of non-stationary time series.
\begin{equation}
\label{arimaprocess}
ARIMA (p, d, q) = ARMA (p+d, q)
\end{equation}
where $p$ is the history of data, $d$ is the difference, and $q$ is the history of errors.
```
import numpy as np
from RecursiveARIMA import RecursiveARIMA
X = np.random.rand(10,5)
recArimaObj = RecursiveARIMA(p=6, d=0, q=6)
recArimaObj.init( X )
for ind in range (100):
x = np.random.rand(1,5)
print "----------------------------"
print "{}#".format (ind+1)
print "----------------------------"
recArimaObj.update ( x )
print recArimaObj.predict( )
```
##### Kalman Filtering
Kalman filter is the continuous form of the forward algorithm of the Hidden Markov model [[Fraser08]](). The general form of the Kalman filter is similar to those in the paper [[WB95]](). This is similar to the formulation in most standard research papers. There are two common formulations of the Kalman filter. This can be understood using the following analogies. In the first case, I know the present in some form and want to predict the future. In the second case, I know the essence of the immediate past and want to determine the present. The use case for the first formulation is used for time series prediction. The use case for the second formulation is used for training, for example, a neural network without back-propagation, thereby working on a near online basis [[OC15]]().
The paper discusses the first case, where we have a set of states and measurements. The state is the main focus, but the next state is not observable from the current state. This can indicate the time series we are tracking. Using the measurements, we augment the estimation of the states.uring dependency between states and measurements. Kalman filter can estimate the next state by using past state and current measurements.
##### Discrete Kalman Filters
The discrete Kalman filter follows the implementation that is described in Figures 1-2 on pages 5 \& 6 of the paper [[WB95]](). This captures the linear relationships in the data. Our estimations fluctuate around the means and covariance. The filter is likely to reach convergence as the data increases, thereby improving filter performance. On the contrary, in the presence of a nonlinear relationship, the error rate increases in the posterior estimates, thereby leading to suboptimal filter performance (under-fitting).
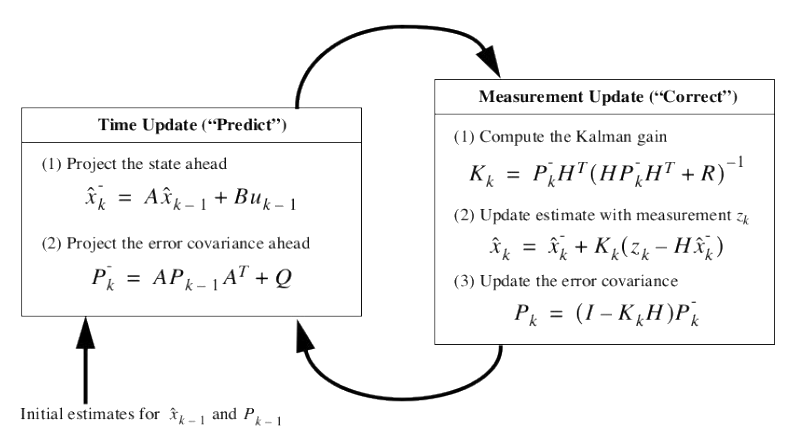
In Figure above from paper [[WB95]](), we have time as $k$, state as $x_k \in R^{n}$, measurement as $z_k \in R^{m}$, matrix $A$ with size $n \times n$, optional control input as $u_k \in R^{l}$, matrix $B$ with size $n \times l$, matrix $H$ with size $m \times n$, covariance matrix as $P_k$, Kalman gain as $k_k$, state noise covariance matrix as $Q$, measurement noise covariance matrix as $R$.
Matrix $A$ represents the relationship between a state and a lagged state. Matrix $B$ is optional and captures the connection between the state and control input. The matrix $H$ captures the relationship between the state and measurement. Measurement innovation, which is the difference between the current measurement and predicted measurement as $z_k - H\hat{x_k}$. If it is zero, then the agreement between the predicted and current measurements is perfect. $K$ is Kalman gain which is used to place weights on the measurement innovation. A lower value of $K$ gives a higher weight on the priori state. Conversely, A higher value of $K$ gives a lower weight on the priori state.
```
import numpy as np
from DiscreteKalmanFilter import DiscreteKalmanFilter
X = np.random.rand(2,2)
Z = np.random.rand(2,2)
dkf = DiscreteKalmanFilter()
dkf.init( X, Z ) #training phase
for ind in range (100):
kf.update( )
x = np.random.rand(1,2)
z = np.random.rand(1,2)
print "----------------------------"
print "{}# {}, {}".format (ind+1, x,z)
print "----------------------------"
print dkf.predict( x, z )
```
##### Extended Kalman Filters
The Extended Kalman filter follows the implementation that is described in Figures 1-2 on pages 8, 9, 10 \& 11 in the paper [[WB95]](). More details on the workings of Extended Kalman filters can be found in the tutorial [[Ter08]](). This captures the nonlinear relationship in the data. Approximating the nonlinear equation using Taylor series to 1st order can produce errors in the posterior estimates, resulting in suboptimal filter performance. The filter makes use of Jacobians and Hessians, thereby mandating the need for differentiable non-linear functions with increased computation cost. This has the same computational complexity as the Unscented Kalman filter.

In Figure above from paper [[WB95]](), we have time as $k$, state as $x_k \in R^{n}$, measurement as $z_k \in R^{m}$, optional control input as $u_k \in R^{l}$, matrix $H$ with size $m \times n$, covariance matrix as $P_k$, Kalman gain as $k_k$, matrices $A, W, H, V$ are Jacobian, and $f$ is a differentiable function.
The matrix $H$ captures the relationship between the state and measurement. Measurement innovation, which is the difference between the current measurement and predicted measurement as $z_k - h(\hat{x_k},0)$. If it is zero, then the agreement between the predicted and current measurements is perfect. $K$ is Kalman gain which is used to place weights on the measurement innovation. A lower value of $K$ gives a higher weight on the priori state. Conversely, A higher value of $K$ gives a lower weight on the priori state.
```
import numpy as np
from ExtendedKalmanFilter import ExtendedKalmanFilter
X = np.random.rand(2,2)
Z = np.random.rand(2,15)
dkf = ExtendedKalmanFilter()
dkf.init( X, Z ) #training phase
for ind in range (100):
dkf.update( )
x = np.random.rand(1,2)
z = np.random.rand(1,15)
print "----------------------------"
print "{}# {}, {}".format (ind+1, x,z)
print "----------------------------"
print dkf.predict( x, z )
```
##### Unscented Kalman Filters
The unscented Kalman filter follows the implementation that is described in Algorithm 3.1 in the paper [[WM00]](). For a thorough understanding of unscented transformation, consult the paper [[Jul02]](). This captures the nonlinear relationship in the data. The approximation uses a higher order Taylor series (linearizing nonlinear equation with Taylor series to 3rd order) for better filter performance. This filter makes use of better sampling to obtain more representative characteristics of the model by using sigma points. Sigma points are extra data points that are chosen within the region surrounding the original data. This accounts for variability by capturing the likely position that data could be given some perturbations. Sampling these points provides richer information about the distribution of the data as it is more ergodic. The filter does not make use of Jacobians and Hessians, thereby allowing the use of differentiable and non-differentiable non-linear functions with increased computation cost. This has the same computational complexity as the Extended Kalman filter.
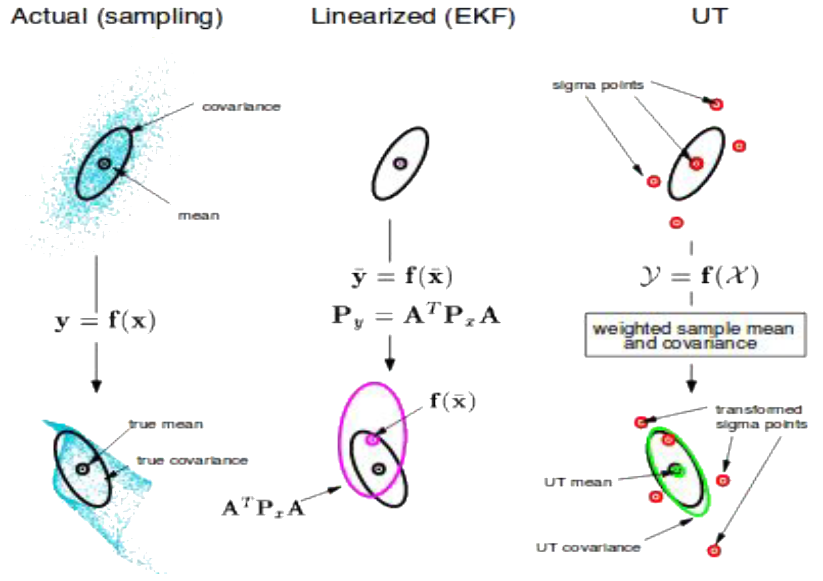
In the Figure above from [[Jul02]](), The actual sampling is done using MCMC and taken as the ground truth for the real distribution of the states and measurements. The extended Kalman filter does not take into account the probability distribution of the underlying process. The unscented Kalman filter makes use of sigma points to capture more information about the underlying dynamic of the process.
```
import numpy as np
from UnscentedKalmanFilter import UnscentedKalmanFilter
X = np.random.rand(2,2)
Z = np.random.rand(2,15)
dkf = UnscentedKalmanFilter()
dkf.init( X, Z ) #training phase
for ind in range (100):
dkf.update( )
x = np.random.rand(1,2)
z = np.random.rand(1,15)
print "----------------------------"
print "{}# {}, {}".format (ind+1, x,z)
print "----------------------------"
print dkf.predict( x, z )
```
We will discuss the Box-Jenkins methodology as a way of selecting appropriate values for the parameter of the model.
Transform data so that a form of stationarity is attained.
E.g taking the logarithm of the data, or other forms of scaling.
Guess values p, d, and q respectively for ARIMA (p, d, q).
Estimate the parameters needed for future prediction.
Perform diagnostics using AIC, BIC, or REC (Regression Error Characteristic Curves) [[BB03]](). It is probably a generalization of Occam’s Razor
### Evaluation
The extended Kalman filter was not evaluated in comparison to other methods. This is because the result is subjective based on the method to estimate the nonlinear function which is a core of the algorithm. One could use a feed-forward network to estimate this relation and as such we fall into yet another issue of second system effects.
It is well-known that ROC is one of the most commonly used evaluation metrics by practitioners of machine learning, and as such it has captured based metrics like Regression Error Characteristic Curves [[BB03]](), MAE, and others, while Bayesian approaches like AIC [[SIG86]](), BIC, Deviance are difficult to interpret by a non-statistician.
A follow-up blog post titled “ROC vs REC: Evaluation measures for classification and Regression ” will be released in the spring of 2020. The article will discuss REC and ROC with intuitive explanations and accompanying source code.
### Conclusion
Accordingly, the context of the problem usually dictates the kind of convergence to aim for among applied scientists. As a result, the algorithms included in the PySmooth packages have provable theoretical guarantees for convergence.
The current implementation uses only the Central processing unit (CPU). Future work would include extending the PySmooth library to take advantage of the Graphics processing unit (GPU) due to the number of matrix multiplication in the Kalman filters. A particle filtering package can be introduced in the next iteration of the software. An implementation detail to enhance numerical stability was using pseudo-inverse in place of exact inverse with minimal effects on performance.
### Acknowledgment
I would like to thank (my mentors) Dr. Ziyuan Gao and Dr. Eugene Yablonsky from the National University of Singapore and Fraser Valley University, BC respectively for providing technical support during the writing of this manuscript. I am grateful to the advanced reading group under the umbrella of [Learn Data Science meetup](https://www.meetup.com/LearnDataScience/) in Vancouver for the lively intellectual conversations on many machine learning topics.
### References
- [[Yul27]]() Yule G. U. “On a Method of Investigating Periodicities in Disturbed Series, with Special Reference to Wolfer’s Sunspot Numbers”. In: Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 226 (1927), pp. 267–298.
- [[Kal60]]() Kalman R. E. “A New Approach to Linear Filtering And Prediction Problems”. In: ASME Journal of Basic Engineering (1960), pp. 35–45.
- [[Mut60]]() Muth J.F. “Optimal properties of exponentially weighted forecasts”. In: Journal of the American Statistical Association 55 (1960), pp. 299–306.
- [[BJ76]]() Box G.E.P. and Jenkins G. M. Time Series Analysis: Forecasting and Control. Holden-Day, 1976.
- [[Rob82]]() Roberts S.A. “A General Class of Holt-Winters Type Forecasting Models”. In: Management Science 28.7 (1982), pp. 808–820.
- [[SIG86]]() Sakamoto Y., Ishiguro M., and Kitagawa G. Akaike Information Criterion Statistics. Reidel Publishing Company, 1986.
- [[Cyb89]]() Cybenko G. “Approximation by Superpositions of a Sigmoidal Function”. In: Mathematics of Control, Signals, and Systems 2 (1989), pp. 303–314.
- [[BJ90]]() Box G.E.P. and Jenkins G. M. Time Series Analysis, Forecasting and Control. Holden-Day, 1990.
- [[HP90]]() Harvey A.C. and Peters S. “Estimation procedures for structural time series models”. In: Journal of Forecasting 9.2 (1990), pp. 89–108.
- [[Hor91]]() Hornik K. “Approximation Capabilities of Multilayer Feedforward Networks”. In: Neural Networks 4.2 (1991), pp. 251–257.
- [[WZ91]]() Wellstead P.E and Zarrop M.B. Self-Tuning Systems: Control and Signal Processing. 1st. Chichester, United Kingdom: John Wiley \& Sons, 1991.
- [[GK92]]() de Gooijer J.G. and Klein A. “On the cumulated multi-step ahead predictions of vector autoregressive moving average processes”. In: International Journal of Forecasting 7.4 (1992), pp. 501–513.
- [[Ham94]]() Hamilton, J. D. Time Series Analysis. 1st edition. Chichester, United Kingdom: Princeton University Press, 1994.
- [[WB95]]() Welch G. and Bishop G. An Introduction to the Kalman Filter. Tech. rep. Chapel Hill, USA, 1995.
- [[Dor96]]() Dorffner G. “Neural Networks for Time Series Processing”. In: Neural Network World 6 (1996), pp. 447–468.
- [[HS97]]() Hochreiter S. and Schmidhuber J. “Long Short-Term Memory”. In: Neural Computation 9.8 (1997), pp. 1735–1780.
- [[FZ98]]() Francq C. and Zakoian J.M. “Estimating linear representations of nonlinear processes”. In: Journal of Statistical Planning and Inference 68.1 (1998), pp. 145–165.
- [[LB98]]() LeCun Y. and Bengio Y. “The Handbook of Brain Theory and Neural Networks”. In: Cambridge, MA, USA: MIT Press, 1998. Chap. Convolutional Networks for Images, Speech, and Time Series, pp. 255–258.
- [[JM99]]() Jain L.C. and Medsker L.R. Recurrent Neural Networks: Design and Applications. 1st edition. Boca Raton, FL, USA: CRC Press, Inc., 1999. ISBN: 0849371813.
- [[WM00]]() Wan E.A. and Merwe R.V.D. “The unscented Kalman filter for nonlinear estimation”. In: Proceedings of the IEEE Adaptive Systems for Signal Processing, Communications, and Control Symposium. 2000, pp. 153–158.
- [[J+01]]() Jones E., Oliphant T., Pearu Peterson, et al. SciPy: Open source scientific tools for Python. 2001. URL: http://www.scipy. org/.
- [[Jul02]]() Julier S.J. “The Scaled Unscented Transformation”. In: Proceedings of the IEEE American Control Conference. 2002, pp. 4555– 4559.
- [[BB03]]() Bi J. and Bennett K.P. “Regression Error Characteristic Curves”. In: Proceedings of the Twentieth International Conference on Machine Learning. 2003, pp. 43–50.
- [[04]]() easy install. 2004. URL: http://setuptools.readthedocs.io/en/latest/easy_install.html.
- [[05]]() NumPy. 2005. URL: http://www.numpy.org/index.html.
- [[08]]() pip. 2008. URL: https://pip.pypa.io/en/stable/.
- [[Ter08]]() Terejanu G.A. Extended Kalman Filter Tutorial. Buffalo, USA, 2008.
- [[WSK10]]() Wang S., Schlobach S., and Klein M.. “What Is Concept Drift and How to Measure It?” In: Knowledge Engineering and Management by the Masses: 17th International Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, pp. 241–256.
- [[12]]() pandas: Python Data Analysis Library. 2012. URL: http://pandas. pydata.org/.
- [[PP14]]() Prasad S.C. and Prasad P. “Deep Recurrent Neural Networks for Time Series Prediction”. In: CoRR abs/1407.5949 (2014). arXiv: 1407.5949. URL: http://arxiv.org/abs/1407.5949.
- [[OC15]]() Ollivier Y. and Charpiat G. “Training recurrent networks online without backtracking”. In: CoRR abs/1507.07680 (2015). arXiv: 1507.07680. URL: http://arxiv.org/abs/1507.07680.
- [[Liu+16]]() Chenghao Liu et al. “Online ARIMA Algorithms for Time Series Prediction”. In: Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. 2016, pp. 1867–1873.
- [[Mal+17]]() Pankaj Malhotra et al. “TimeNet: Pre-trained deep recurrent neural network for time series classification”. In: CoRR abs/1706.08838 (2017). arXiv: 1706.08838. URL: http://arxiv.org/abs/1706.08838.
- [[Odo17]]() Kenneth Odoh. PySmooth: an open source object-oriented library for time series analysis in Python. 2017. URL: https://github.com/kenluck2001/pySmooth.
- [[TL17]]() Taylor S.J. and Letham B. Forecasting at Scale. 2017. URL: https://doi.org/10.7287/peerj.preprints.3190v2.
- [[Fraser08]]() Fraser A. M. 2008. Hidden Markov Models and Dynamical Systems. Society for Industrial and Applied Mathematics, Philadelphia, PA, USA.
### **How to Cite this Article**
```
BibTeX Citation
@article{kodoh2019a,
author = {Odoh, Kenneth},
title = {PySmooth: A time series library from first principles},
year = {2019},
note = {https://kenluck2001.github.io/blog_post/pysmooth_a_time_series_library_from_first_principles.html}
}
```
15/18
Please feel free to donate to support my work by clicking